近期，安光所大气光学研究中心朱文越研究员课题组提出非Kolmogorov湍流折射率结构常数的等效方法，该方法建立了Kolmogorov湍流折射率结构常数与非Kolmogorov湍流折射率结构常数之间的等效关系，这一成果发表在美国光学学会（OSA）近期出版的 optics express (2015，23(18)，23004-23012)上。

    湍流引起的大气折射率的随机起伏导致了在其中传播的光波的波前发生畸变，破坏光的相干性，给光通信、光学遥感、光学成像等应用带来困扰，严重制约了激光工程的应用。折射率结构常数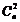用于描述湍流强度的大小，其具有明显的日变化特征和高度变化特征。目前存在的湍流折射率结构常数的测量数据和模式都是基于Kolmogorov的湍流统计理论得到的，然而，随着研究的不断发展，人们发现大气湍流并非总是符合Kolmogorov统计特征的，于是非Kolmogorov湍流的概念被提了出来。在非Kolmogorov湍流大气中光传播效应的研究中仍采用折射率结构常数来描述湍流强度的大小，但结构常数的量纲不再是Kolmogorov湍流时的“m-2/3”而是与结构函数的幂率“g”相关，表示为“m-g”，称为一个量纲不固定的参量，不再适合描述湍流起伏的强度。这给非Kolmogorov湍流强度的描述以及非Kolmogorov湍流大气中光传播特性的分析带来严重的困扰。除此之外，找出Kolmogorov湍流与非Kolmogorov湍流之间的关系也是光大气传播研究中亟待解决的问题。

　　文中，基于湍流结构函数和折射率起伏方差建立了非Kolmogorov湍流折射率结构常数与Kolmogorov湍流折射率结构常数之间的等效关系，并从实验上验证了该结果的正确性。该等效关系能够将非Kolmogorov结构常数表示成Kolmogorov结构常数，湍流外尺度和幂率的函数。一方面避免了使用非Kolmogorov折射率结构常数时由于其量纲的不固定给传播研究带来的困扰，另一方面该等效关系能够将Kolmogorov湍流大气中的光传播特性与非Kolmogorov湍流大气中的光传播特性联系起来。除此之外，我们还可以通过该关系式并结合外尺度模型，谱幂率模型以及已有的Kolmogorov结构常数廓线模型建立非Kolmogorov湍流结构常数的廓线模型。

　　全文链接https://www.osapublishing.org/oe/fulltext.cfm?uri=oe-23-18-23004