中科院合肥研究院固体所物质计算科学研究室张国仁博士与德国于利希研究中心（FZJ）Pavarini教授合作，在4d关联体系Ca₂RuO₄的磁Higgs模和轨道序的稳定性研究方面取得新进展。结合局域密度近似+动力学平均场（LDA+DMFT）和多体微扰论方法，确认了Ca₂RuO₄中xy 型轨道序的鲁棒性（Robustness），并指出该体系中实验上发现的磁Higgs模与xy型轨道序是兼容的，并不需要基于强自旋-轨道耦合极限的图像来解释。相关结果以“Higgs mode and stability of xy-orbital ordering in Ca2RuO₄”为题发表在《物理评论B》上。

　　相对于3d关联电子体系（自旋-轨道耦合常数在20至50 meV之间），4d体系拥有较强的自旋-轨道耦合（相关常数在100至200 meV之间）。但是4d体系的自旋-轨道耦合又不像5d或4f体系那样相对于晶体场占主导地位。这导致已有研究中出现了相互矛盾的物理图像：把自旋-轨道耦合当作微扰处理（甚至忽略）的弱耦合图像和强自旋-轨道耦合极限图像。因此，非常有必要厘清自旋-轨道耦合在决定4d关联电子体系物性时的重要程度。张国仁博士前期已与合作者在相关方面进行了深入的研究，并取得了一系列进展。

　　   Ca₂RuO₄是4d关联电子体系中的代表性材料之一。早期对其磁性的研究是基于Ru⁴⁺局域磁矩即弱自旋-轨道耦合的图像来进行讨论的。后来，一种基于强自旋-轨道耦合极限的图像-Van Vleck磁性研究变得流行起来。这种图像的出发点是局域离子总角动量J_tot为零的基态。这一基态的一个典型特征是xy, yz, xz三个轨道被同等占据, n_xy:n_yz:n_xz=1:1:1。这和LDA+DMFT计算所得的xy-型轨道序（n_xy: n_yz:n_xz=2:1:1）基态不一致。而xy-型轨道序则是被一系列角分辨光电子谱所证实的。尽管如此，这种基于强自旋-轨道耦合极限的图像在解释Ca₂RuO₄磁性时仍然非常流行。其中一个重要的原因是，基于这种图像最近实验上发现的磁Higgs模可以得到较好的解释。那么在Ca₂RuO₄中自旋-轨道到底起到什么作用及磁Higgs模和xy型轨道序是否能够兼容是非常值得研究的问题。

　　    针对这些问题，研究人员采用LDA+DMFT结合微扰论的方法研究了Ca₂RuO₄中xy型轨道序的鲁棒性和磁Higgs模。结果表明，只有当体系的晶体场减少至真实材料的一半以下时，才会发生自旋-轨道耦合从微扰到非微扰的渡越行为（图1）。也就是说，Ca₂RuO₄中的xy型轨道序是非常稳定的。基于xy型轨道序这一基态，研究人员通过微扰论方法计算了Ca₂RuO₄中磁交换常数和单离子各向异性张量，确定了自旋-轨道耦合在能量架构中的地位：尽管相对于晶体场自旋-轨道耦合处于微扰地位，但是由它决定的单离子各项异性却远大于离子间的超交换作用。在这样的能量层次架构下，研究人员计算了Ca₂RuO₄的磁横向pseudo-Goldstone和纵向Higgs激发模及他们的磁密度（图2）。结果表明，实验上发现的处于50 meV的磁信号非常有可能是Higgs模，而不是偶数个横向模激发。更重要的是，Higgs模可以在xy轨道序图像下很好地得到解释。

　　该项工作得到了国家自然科学基金的资助，相关的LDA+DMFT计算是在德国于利希研究中心超级计算机系统JUWELS上完成的。

　　文章链接：https://journals.aps.org/prb/abstract/10.1103/PhysRevB.101.205128

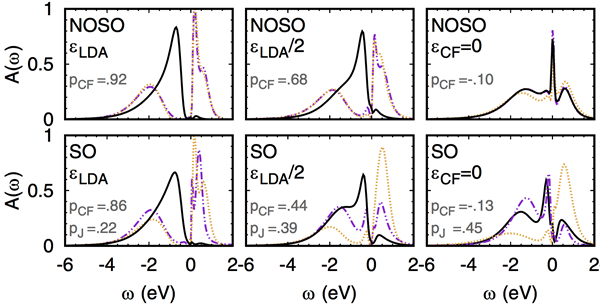
图1. 不同晶体场下的谱函数，用于展示自旋-轨道耦合作用从微扰到非微扰的渡越行为。左图：真实晶体场；中图：晶体场减少一半；右图：晶体场为零。

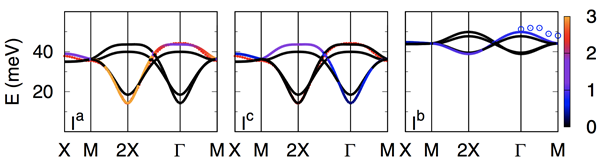
　　图2. Ca₂RuO₄中横向pseudo-Goldstone（左及中图）和纵向Higgs模（右图）。实线，计算值；点线，实验上具有最大磁密度的横向模；空圆圈，实验所得的Higgs模。